Python 標準ライブラリ random 擬似乱数

2021-04-10

ライブラリrandomを使うとPythonで乱数を使うことができます。

整数値の乱数を取得する例

import random
random.seed(0)
random.randrange(5) # => 3

ranomの内部状態を設定するメソッド

再現性のある結果が欲しい場合random.seed(0)等で乱数のシードを固定しておく。

seed(a=None, version=2) 乱数生成の初期化

random.seed()
random.seed(0)

getstate() 乱数生成器の内部状態のオブジェクト取得

state = random.getstate()

setstate(state) 乱数生成器の内部状態の設定

state = random.getstate()
random.setstate(state)

度数分布のグラフを出力する準備

以降で乱数の出力結果をヒストグラムでみたいので以下の関数を定義しておく。

import matplotlib.pyplot as plt
def hist_plot(data, bins, xticks):
    fig = plt.figure()
    ax = fig.add_subplot(1, 1, 1)
    ax.hist(data, bins=bins)
    ax.set_xticks(xticks)

整数の乱数

randrange(stop) 0以上～stop未満の整数の乱数

random.randrange(10) # => 0～9の整数
hist_plot([random.randrange(10) for x in range(1000)], 10 , range(0,10))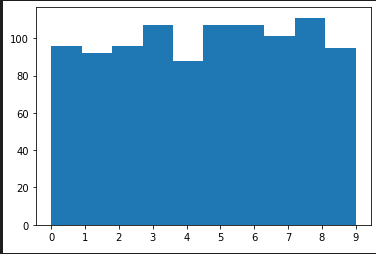

random.randrange(10)の度数分布図

randrange(start, stop[, step]) range(start, stop[, step])の範囲にある整数の乱数

random.randrange(2, 9) # => 2～8の整数
hist_plot([random.randrange(2, 9) for x in range(1000)], 7 , range(2,9))

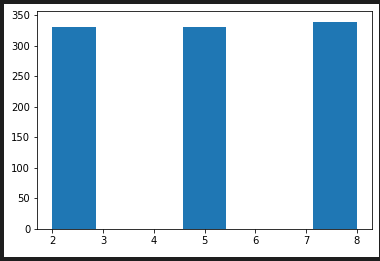
random.randrange(2, 9, 3) # => 2～8の整数3つおき(=> 2, 5, 8)
hist_plot([random.randrange(2, 9, 3) for x in range(1000)], 7 , range(2,9))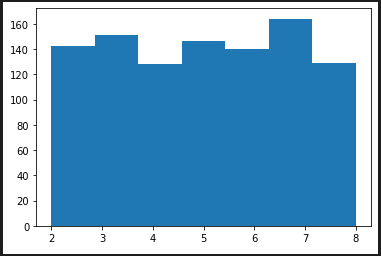

random.randrange(2, 9)の度数分布図

random.randrange(2, 9, 3)の度数分布図

randint(a, b) a<=N<=bの整数の乱数 randrange(a, b+1)

random.randint(2,8) # => 2～8の整数
hist_plot([random.randint(2,8) for x in range(1000)], 7 , range(2,9))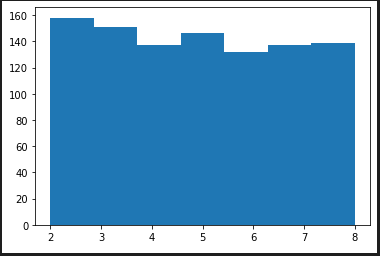

random.randint(2, 8)の度数分布図

getrandbits(k) kビットで表現できる整数の乱数

random.getrandbits(3) # => 0b000～0b111

[random.getrandbits(3) for x in range(10)]
# => [7, 7, 0, 2, 5, 3, 1, 2, 6, 2]

[bin(random.getrandbits(3)) for x in range(10)]
# => ['0b110', '0b0', '0b110', '0b1', '0b111', '0b11', '0b11', '0b0', '0b0', '0b101']

hist_plot([random.getrandbits(3) for x in range(1000)], 8 , range(0,8))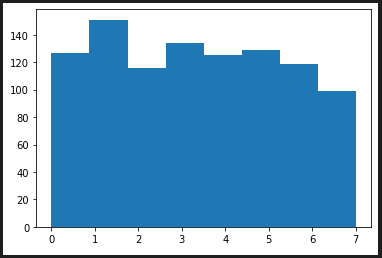

random.getrandbits(3)の度数分布図

ランダムな要素の取り出し

choice(seq) シーケンスからランダムに要素取得

random.choice('abc') # => 'a', 'b', 'c'
random.choice([1, 3, 7, 1]) # => 1, 3, 7

choices(population, weights=None, *, cum_weights=None, k=1) 重複ありの要素抽出

重みweights,cum_weightsを付けてシーケンスからk個を取り出す。 weightsは相対的な比率で、cum_weightsは累積的な値で重みを指定する。

population = [1, 2, 3]
random.choices(population) # => [1], [2], [3]
random.choices(population, k=2) # => [1,1], [1,2]等

#重みづけで取得(相対的)
random.choices(population, weights=[60,10,20]) # => [1], [2], [3]
hist_plot( [ random.choices(population, weights=[60,10,20])[0] for x in range(1000) ], 3 , range(1,3))

#重みづけで取得(累積的)
random.choices(population, cum_weights=[60,70,90]) # => [1], [2], [3]
hist_plot(  [ random.choices(population, cum_weights=[60,70,90])[0] for x in range(1000) ], 3 , range(1,3))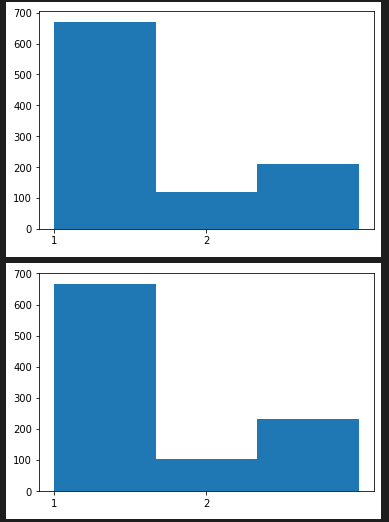

random.choices()の度数分布図

shuffle(x) シーケンスのシャッフル (ミュータブルなシーケンスそのものの並び替え)

items = list(range(10))
random.shuffle(items)
items # => [6, 3, 8, 4, 5, 1, 0, 2, 7, 9]

sample(population, k, *, counts=None) 母集団からk個の要素のリストを作成

countsで各要素の出現回数を指定できる。

items = list(range(10))
random.sample(items,2) # => [3, 5]等

# countsの指定で母集団各要素の選択回数を指定できる
random.sample([1,2,3], 2, counts=[5,1,4]) # => [1, 3]等
# 以下と同じ
random.sample([1,1,1,1,1,2,3,3,3,3], 2) # => [1, 3]等

浮動小数の乱数

random() 0以上1未満の小数 [0.0, 1.0)

random.random() # => 0.8444218515250481

hist_plot([random.random() for x in range(10000) ], 50 , [0.1*x for x in range(0,11)])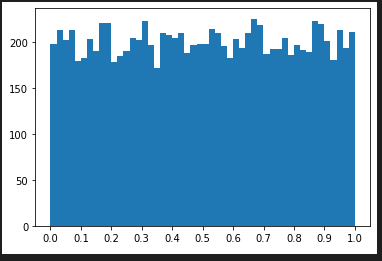

random.random()の度数分布図

random.uniform(a, b) a以上b以下 [a,b](またはb以上a以下b [b,a])の小数

random.uniform(3, 8) # => 7.323203944644748

hist_plot([random.uniform(3, 8)  for x in range(10000) ], 50 , [0.1*x+3.0 for x in range(0,11)])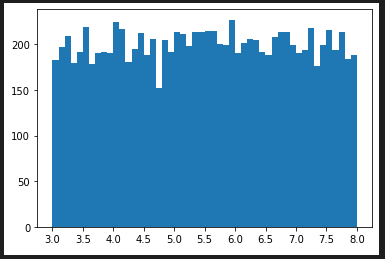

random.uniform(3, 8)の度数分布図

triangular(low, high, mode) low以上high以下で最頻値modeの小数

# デフォルトはlow=0,high=1,mode=(low+high)/2
random.triangular() # = > 0.5811208765762167

hist_plot([random.triangular()  for x in range(10000) ], 50 , [0.1*x for x in range(0,11)])
hist_plot([random.triangular(3,5)  for x in range(10000) ], 50 , [0.2*x+3.0 for x in range(0,11)])
hist_plot([random.triangular(3,5,4.5)  for x in range(10000) ], 50 , [0.2*x+3.0 for x in range(0,11)])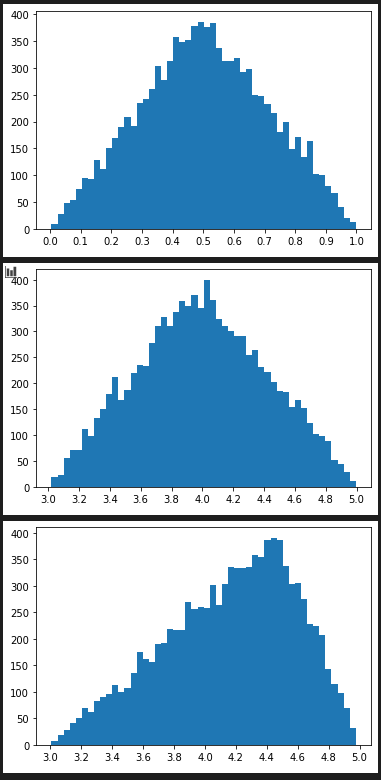

random.triangular()の度数分布図

betavariate(alpha, beta) ベータ分布(beta distribution)

random.betavariate(2, 2) # = > 0.5395630434906871

hist_plot([random.betavariate(2, 2)  for x in range(10000) ], 50 , [0.1*x for x in range(0,11)])
hist_plot([random.betavariate(0.5, 0.5)  for x in range(10000) ], 50 , [0.1*x for x in range(0,11)])
hist_plot([random.betavariate(5, 1)  for x in range(10000) ], 50 , [0.1*x for x in range(0,11)])
hist_plot([random.betavariate(1, 3)  for x in range(10000) ], 50 , [0.1*x for x in range(0,11)])
hist_plot([random.betavariate(2, 5)  for x in range(10000) ], 50 , [0.1*x for x in range(0,11)])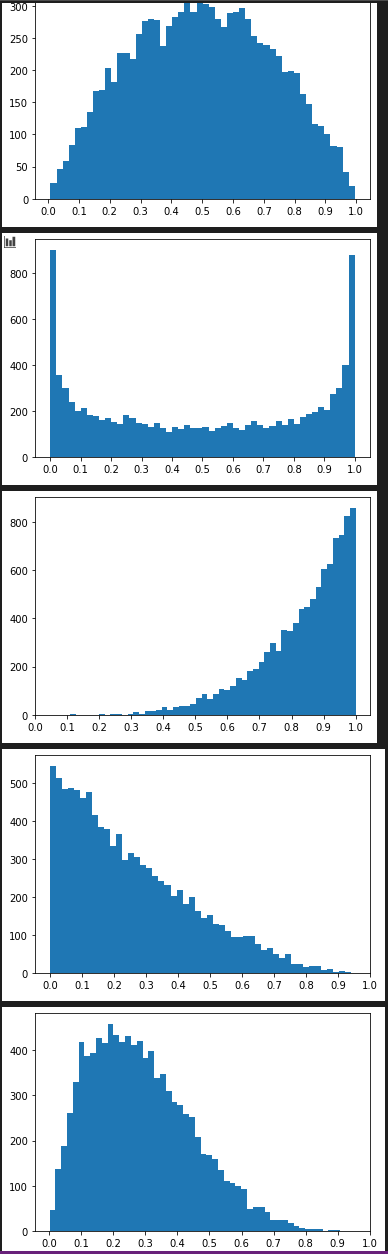

$$ ベータ分布の確率密度関数: f(x;\alpha ,\beta )={\frac {x^{\alpha -1}(1-x)^{\beta -1}}{B(\alpha ,\beta )}} \ for \ x \in [0,1] \\ 期待値: E(x)=\frac{\alpha}{\alpha + \beta} \ \ \ 分散: V(x)={\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}} \\ ベータ関数: \mathrm {\mathrm {B} } (x,y)=\int _{0}^{1}t^{x-1}(1-t)^{y-1}\,dt $$

random.betavariate()の度数分布図

expovariate(lambd) 指数分布 (exponential distribution)

random.expovariate(10) # = > 0.0443397045417289

hist_plot([random.expovariate(10)  for x in range(10000) ], 50 , [x*0.1 for x in range(0,10)])
hist_plot([random.expovariate(1)   for x in range(10000) ], 50 , [x for x in range(0,10)])
hist_plot([random.expovariate(0.1) for x in range(10000) ], 50 , [x*10 for x in range(0,10)])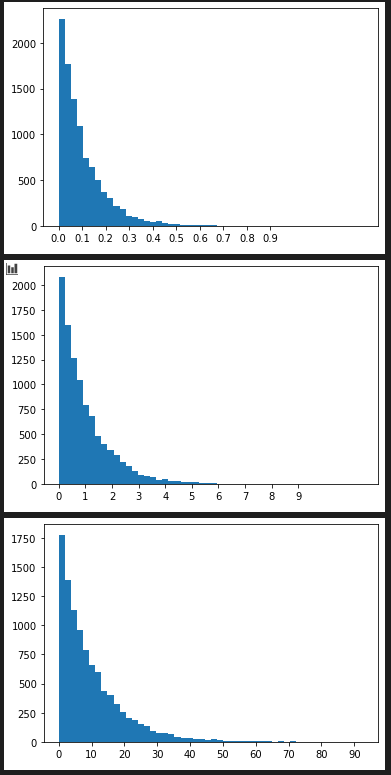

$$ 指数分布の確率密度関数: f(x;\lambda )=\lambda e^{-\lambda x} \ for \ x \in [0,\infty) \\ 期待値: E(x)={\frac {1}{\lambda }} \ \ \ \ \ \ 分散: V(x)={\frac {1}{\lambda ^{2}}} $$

random.expovariate()の度数分布図

gammavariate(alpha, beta) ガンマ分布(gamma distribution)

random.gammavariate(9, 0.5) # = > 4.555121091194622

hist_plot([random.gammavariate(9, 0.5)  for x in range(10000) ], 50 , [x for x in range(0,10)])
hist_plot([random.gammavariate(1, 2)  for x in range(10000) ], 50 , [x for x in range(0,10)])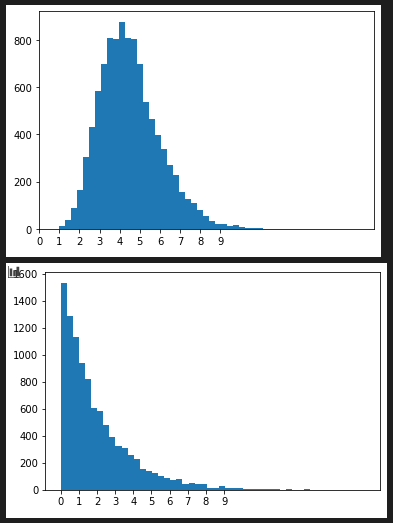

$$ ガンマ分布の確率密度関数: f(x)={\frac {1}{\Gamma (\alpha)\,\beta ^{\alpha}}}x^{\alpha-1}e^{-x/\beta }\ \ \ \ \mathrm \ x \in (0,\infty) \\ \\ 期待値: E(x)={\alpha}{\beta } \ \ \ \ \ \ 分散: V(x)={\alpha}{\beta }^2 $$

random.gammavariate()の度数分布図

gauss(mu, sigma) ガウス分布(正規分布) (Gaussian distribution)

muは平均、 sigma は標準偏差。後にでてくるnormalvariate()よりも少し高速。

random.gauss(0, 1) # = > 0.31367378413426494

hist_plot([random.gauss(0,1)  for x in range(10000) ], 50 , [x for x in range(-5,6)])
hist_plot([random.gauss(2,1)  for x in range(10000) ], 50 , [x for x in range(-5,6)])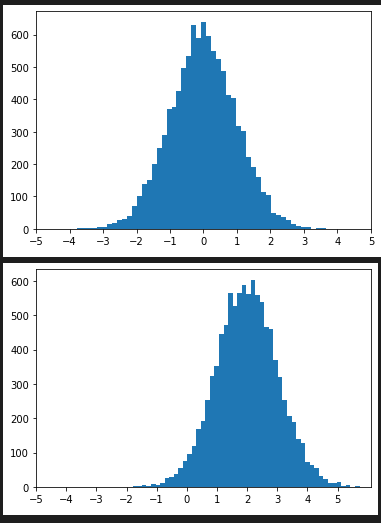

$$ ガウス分布の確率密度関数: f(x)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\exp \!\left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\quad (x\in \mathbb {R} ) \\ 期待値: E(x)={\mu} \ \ \ \ \ \ 分散: V(x)={\sigma}^2 $$

random.gauss()の度数分布図

lognormvariate(mu, sigma) 対数正規分布 (log-normal distribution)

random.lognormvariate(0, 0.01) # = >1.0042626445054275

hist_plot([random.lognormvariate(0,0.01)  for x in range(10000) ], 50 , [x for x in range(0,4)])
hist_plot([random.lognormvariate(0,0.1)  for x in range(10000) ], 50 , [x for x in range(0,4)])
hist_plot([random.lognormvariate(0,0.5)  for x in range(10000) ], 50 , [x for x in range(0,4)])
hist_plot([random.lognormvariate(0,1)  for x in range(10000) ], 50 , [x for x in range(0,4)])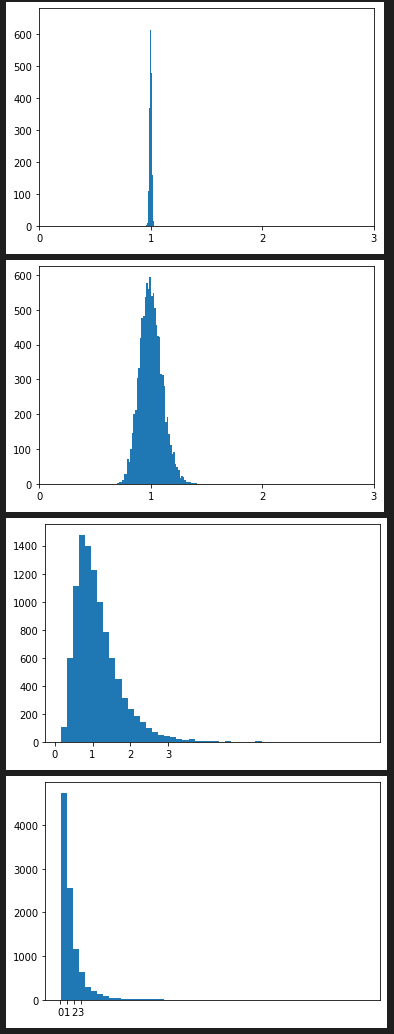

$$ 対数正規分布の確率密度関数: f(x)={\frac {1}{{\sqrt {2\pi }}\sigma x}}\exp \left(-{\frac {(\ln x-\mu )^{2}}{2\sigma ^{2}}}\right) \ \ x \in (0,\infty) \\ 期待値: E(x)=e^{\mu +\sigma ^{2}/2} \ \ \ \ \ \ 分散: V(x)==e^{2\mu +\sigma ^{2}}(e^{\sigma ^{2}}-1) $$

random.lognormvariate()の度数分布図

normalvariate(mu, sigma) 正規分布(ガウス分布) (normal distribution)

gauss()と同様。

random.normalvariate(0, 1) # = > -0.3401010161409137

hist_plot([random.normalvariate(0,1)  for x in range(10000) ], 50 , [x for x in range(-5,6)])
hist_plot([random.normalvariate(2,1)  for x in range(10000) ], 50 , [x for x in range(-5,6)])

gauss()の方がnormalvariate()よりも少しだけ高速。

%timeit -r 7 -n 100000 random.gauss(0,1)
# => 853 ns ± 162 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

%timeit -r 7 -n 100000 random.normalvariate(0,1)
# => 985 ns ± 172 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)

vonmisesvariate(mu, kappa)　フォン・ミーゼス分布 (von Mises distribution)

0から2*piラジアンまでの角度方向の分布。平均muが一番多くなる。kappaは濃度パラメータで、ゼロだと一様な分布。

import math
random.vonmisesvariate(0, 1) # = > 6.087179444930305

hist_plot([random.vonmisesvariate(0,0)  for x in range(10000) ], 50 , [x for x in range(0,7)])
hist_plot([random.vonmisesvariate(0,1)  for x in range(10000) ], 50 , [x for x in range(0,7)])
hist_plot([random.vonmisesvariate(0,2)  for x in range(10000) ], 50 , [x for x in range(0,7)])

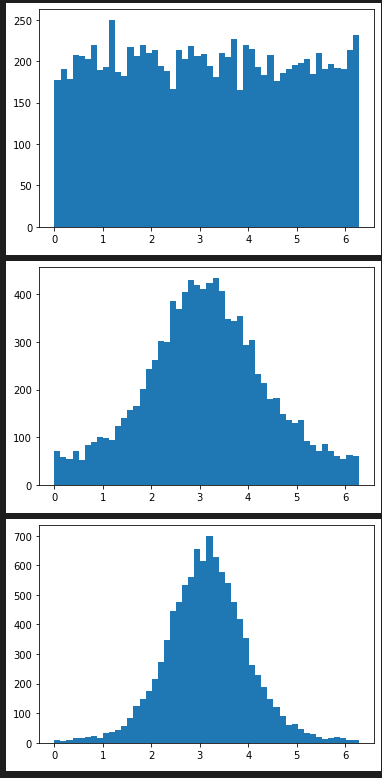
hist_plot([random.vonmisesvariate(math.pi,0)  for x in range(10000) ], 50 , [x for x in range(0,7)])
hist_plot([random.vonmisesvariate(math.pi,1)  for x in range(10000) ], 50 , [x for x in range(0,7)])
hist_plot([random.vonmisesvariate(math.pi,2)  for x in range(10000) ], 50 , [x for x in range(0,7)])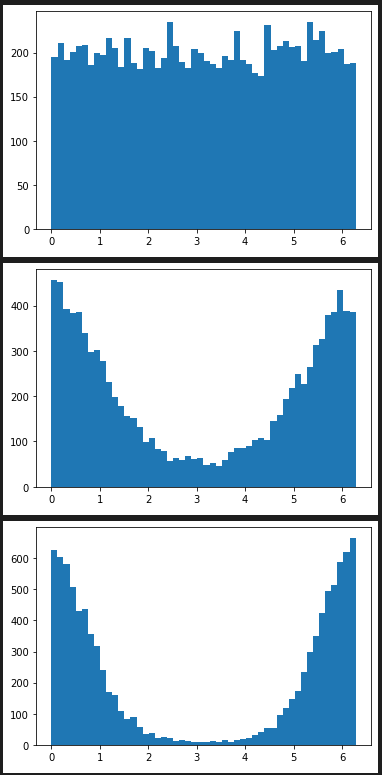

$$ フォン・ミーゼス分布の確率密度関数: F(\theta )=\left\{2\pi I_{0}(\kappa )\right\}^{-1}\left[\theta I_{0}(\kappa )+2\left\{\sum _{j=0}^{\infty }{\frac {I_{j}(\kappa )\sin(j(\theta -\mu ))}{j}}\right\}\right] \\ \mu \in [0, 2\pi), \ \ \kappa \in [0, \infty) \\ f(\theta )={\frac {\exp\{\kappa \cos(\theta -\mu )\}}{2\pi I_{0}(\kappa )}}\\ I_{j}(\kappa )=\left({\frac {\kappa }{2}}\right)^{j}\sum _{i=0}^{\infty }{\frac {\left({\frac {\kappa ^{2}}{4}}\right)^{i}}{i!\Gamma (j+i+1)}} \ \ (j次の第一種変形ベッセル関数) \\ $$

random.vonmisesvariate()の度数分布図

paretovariate(alpha) パレート分布 (Pareto distribution)

def hist_plot_rim(data, bins, xticks, xlim):
    fig = plt.figure()
    ax = fig.add_subplot(1, 1, 1)
    ax.hist(data, bins=bins)
    ax.set_xticks(xticks)
    ax.set_xlim(*xlim)

random.paretovariate(10) #=> 1.0005914562417035

hist_plot_rim([random.paretovariate(1)  for x in range(10000) ], 200 , [0.5*x+1 for x in range(0,10)], [0.5,3])
hist_plot_rim([random.paretovariate(2)  for x in range(10000) ], 200 , [0.5*x+1 for x in range(0,10)], [0.5,3])
hist_plot_rim([random.paretovariate(3)  for x in range(10000) ], 200 , [0.5*x+1 for x in range(0,10)], [0.5,3])
hist_plot_rim([random.paretovariate(5)  for x in range(10000) ], 200 , [0.5*x+1 for x in range(0,10)], [0.5,3])
hist_plot_rim([random.paretovariate(10)  for x in range(10000) ],200 , [0.5*x+1 for x in range(0,10)], [0.5,3])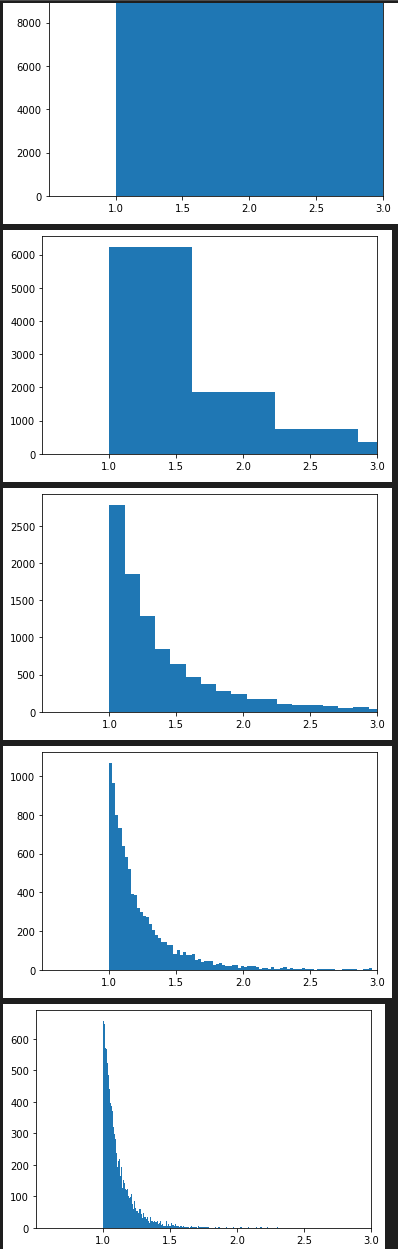

$$ パレート分布の確率密度関数: f_{X}(x)={\begin{cases}{\frac {\alpha}{x^{\alpha +1}}}&x\geq 1,\\0&x<1.\end{cases}} \\ 期待値: E(x)={\frac{\alpha}{\alpha - 1}} \ \ \alpha \in (1, \infty) \ \ \ \ \ \ 分散: V(x)={\frac{\alpha}{(\alpha-1)^2(\alpha-2)}} \ \ \alpha \in (2, \infty) $$

random.paretovariate()の度数分布図

weibullvariate(alpha, beta) ワイブル分布 (Weibull distribution)

alphaはスケールパラメータ、betaは形状パラメータ。

hist_plot([random.weibullvariate(1, 1)  for x in range(10000) ], 50 , [x*0.1 for x in range(0,10)])
hist_plot([random.weibullvariate(1, 2)  for x in range(10000) ], 50 , [x*0.1 for x in range(0,10)])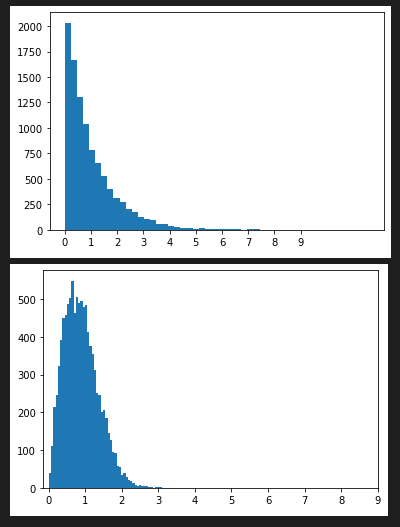

$$ ワイブル分布の確率密度関数: f(x)={\frac {\beta}{\alpha }}\left({\frac {x}{\alpha }}\right)^{\beta-1}\exp \left\{-\left({\frac {x}{\alpha }}\right)^{\beta}\right\} \\ 期待値: E(x)=\alpha \Gamma \left(1+{\frac {1}{\beta}}\right) \ \ \ \ \ \ 分散: V(x)=\operatorname {var} (X)=\alpha ^{2}\left[\Gamma \left(1+{\frac {2}{\beta}}\right)-\left(\Gamma \left(1+{\frac {1}{\beta}}\right)\right)^{2}\right] $$

random.weibullvariate()の度数分布図

その他のメソッド

randbytes(n) ランダムなバイト生成

random.randbytes(5) # => b'\xcd\x07,\xd8b'