Python 標準ライブラリ statistics 数理統計

2021-04-10

statisticsはPythonの標準で用意されている統計用の各種機能を持ったライブラリです。平均や分散、正規分布の取り扱いを行う事ができます。

サンプルの正規分布データ

以降で使うため、サンプルの正規分布のデータを用意しておきます。

import random
random.seed(0)

# 平均2 標準偏差3 の正規分布乱数100万個
data = [random.gauss(2,3)  for x in range(1000000) ]

各種の統計量の計算用関数

mean(data) 算術平均(相加平均)

statistics.mean(data) # => 2.003101708077845

from fractions import Fraction
statistics.mean([Fraction(1, 4), Fraction(1, 5), Fraction(1, 6), Fraction(1, 7)])
# => Fraction(319, 1680)

from decimal import Decimal
statistics.mean([Decimal("0.1"), Decimal("0.2"), Decimal("0.3"), Decimal("0.4")])
# => Fraction(319, 1680)

$$ m={\frac {1}{n}}\textstyle \sum \limits _{k=1}^{n}x_{k}={\dfrac {x_{1}+x_{2}+\cdots +x_{n}}{n}} $$

fmean(data) 浮動小数の算術平均(相加平均)

statistics.fmean(data) # => 2.003101708077845

from fractions import Fraction
statistics.fmean([Fraction(1, 4), Fraction(1, 5), Fraction(1, 6), Fraction(1, 7)])
# => 0.18988095238095237

from decimal import Decimal
statistics.fmean([Decimal("0.1"), Decimal("0.2"), Decimal("0.3"), Decimal("0.4")])
# => 0.25

geometric_mean(data) 幾何平均

statistics.geometric_mean(filter(lambda x: x > 0, data)) # => 2.348852376873991
statistics.geometric_mean([24,9,125]) # => 30.000000000000004

$$ G = \left(\textstyle \prod \limits _{i=1}^{n}x_{i}\right)^{\frac {1}{n}}={\sqrt[{n}]{x_{1}x_{2}\dotsb x_{n}}} $$

harmonic_mean(data) 調和平均

statistics.harmonic_mean(filter(lambda x: x > 0, data)) # => 0.5049265887002424
statistics.harmonic_mean([40, 60]) #=> 48.0

$$ H={\frac {n}{\sum \limits _{i=1}^{n}{\frac {1}{x_{i}}}}}={\frac {n}{{\frac {1}{x_{1}}}+{\frac {1}{x_{2}}}+\cdots +{\frac {1}{x_{n}}}}} $$

median(data) メジアン(中央値)

statistics.median(data) # => 2.0027491546951763
statistics.median([1,2,5,6,9]) # => 5
statistics.median([1,2,5,6,8,9]) # => 5.5

$$ \mathrm {Q} _{\frac {1}{2}}= {\begin{cases} { \text{昇順に要素を並べた時の} \frac{n+1}{2} \text{番目 (要素数nが奇数)} } \\ { \text{昇順に要素を並べた時の} \frac{n}{2} \text{番目と} \frac{n+2}{2} \text{番目の平均 (要素数nが偶数)} } \end{cases}} $$

median_low(data) メジアン(中央値か小さい方)

statistics.median_low(data) # => 2.002745121193964
statistics.median_low([1,2,5,6,9]) # => 5
statistics.median_low([1,2,5,6,8,9]) # => 5

median_high(data) メジアン(中央値か大きい方)

statistics.median_high(data) # => 2.002753188196389
statistics.median_high([1,2,5,6,9]) # => 5
statistics.median_high([1,2,5,6,8,9]) # => 6

median_grouped(data, interval=1) 補完したメジアン

statistics.median_grouped(data) # => 1.502753188196389
statistics.median_grouped([1,2,3]) # => 2.0
statistics.median_grouped([1,2,2]) # => 1.75
statistics.median_grouped([1,2,2,3]) # => 2.0
statistics.median_grouped([1,2,2,3,3]) # => 2.25

mode(data) 最頻値 (複数ある場合は最初に登場したもの)

statistics.mode(data) # => 4.825146214041993
statistics.mode([1,1,2,3,3,3,3,4,5,5,6,6,6,6]) # => 3
statistics.mode(['a','a','b','b','b','c','c','c','d']) # => 'b'

multimode(data) 複数の最頻値

statistics.multimode(data) # => 2.025128538506135, 3.5108901691355143,…
statistics.multimode([1,1,2,3,3,3,3,4,5,5,6,6,6,6]) # => [3, 6]
statistics.multimode(['a','a','b','b','b','c','c','c','d']) # => ['b', 'c']

pstdev(data, mu=None) 母標準偏差(データが母集団の場合に使用する)

statistics.pstdev(data) # => 2.9998192000383304

pvariance(data, mu=None) 母分散(データが母集団の場合に使用する)

statistics.pvariance(data) # => 8.998915232918609

stdev(data, xbar=None) 標本標準偏差(標本から計算した不偏分散の平方根)

random.seed(0)
loop = 10
stdevs = []
for i in range(loop):
    sample_data = random.sample(data,10000)
    stdevs.append(statistics.stdev(sample_data))

statistics.mean(stdevs)
# => 3.013484862216274

variance(data, xbar=None) 標本分散 (標本から不偏分散を計算)

random.seed(0)
loop = 10
variances = []
for i in range(loop):
    sample_data = random.sample(data,10000)
    variances.append(statistics.variance(sample_data))

statistics.mean(variances)
# => 9.081665198551224

quantiles(data, *, n=4, method=‘exclusive’) データの分割

tiles = statistics.quantiles(data)
tiles # => [-0.017355856620645316, 2.0027491546951763, 4.026714654241148]

len(data) # => 1000000
sum([(1 if x <= tiles[0] else 0) for x in data]) # => 250000
sum([(1 if tiles[0] < x and x <= tiles[1] else 0) for x in data]) # => 250000
sum([(1 if tiles[1] < x and x <= tiles[2] else 0) for x in data]) # => 250000
sum([(1 if tiles[2] < x else 0) for x in data]) # => 250000

# 10分割
tiles = statistics.quantiles(data, n=10)
tiles # => [-1.8438196482118687, -0.5228557865524757, 0.42921456410951775,
#  1.2410669510576056, 2.0027491546951763, 2.763201232068235,
#  3.578172336618947, 4.5272166210547855, 5.847496513505737]

import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.hist(data, bins=50)
ax.set_xticks([x for x in range(-5,8)])

tiles = statistics.quantiles(data)
ax.axvline(tiles[0], color='r', linestyle='-')
ax.axvline(tiles[1], color='r', linestyle='-')
ax.axvline(tiles[2], color='r', linestyle='-')

plt.show()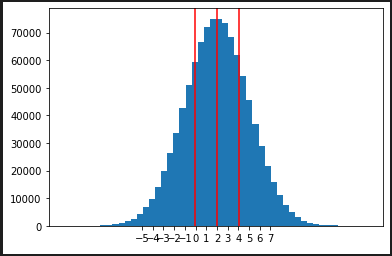

正規分布の分割

正規分布クラス NormalDist

NormalDist(mu=0.0, sigma=1.0) 平均mu、標準偏差sigmaの正規分布

nd = statistics.NormalDist(1.0, 2.0)

nd # => NormalDist(mu=1.0, sigma=2.0)
nd.mean # => 1.0 平均
nd.median # => 1.0 中央値
nd.mode # => 1.0 最頻値
nd.stdev # => 2.0 標準偏差
nd.variance # => 4.0 分散

statistics.NormalDist.from_samples(data) データから正規分布を推測

statistics.NormalDist.from_samples(data)
# => NormalDist(mu=2.003101708077845, sigma=2.9998206999490558)

samples(n, *, seed=None) n個のランダムなサンプル

nd.samples(2) # => [0.2114438019581495, 1.6427031628717423]

pdf(x) 確率密度関数(probability density function)

nd.pdf(0) # => 0.17603266338214976
nd.pdf(1) # => 0.19947114020071635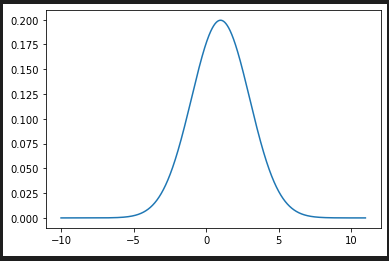

$$ f(x)={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\exp \!\left(-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}\right)\quad (x\in \mathbb {R} ) $$

正規分布の確率密度関数

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
x = [-10+0.01*v for v in range(2100)]
y = [nd.pdf(v) for v in x]
plt.plot(x, y)
plt.show()

cdf(x) 累積分布関数 (cumulative distribution function)

nd.cdf(0) # => 0.30853753872598694
nd.cdf(1) # => 0.5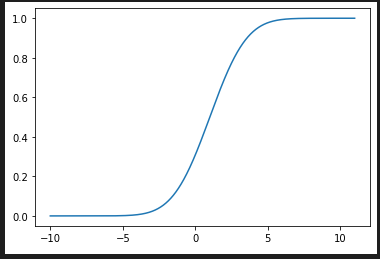

$$ F(x) =\int _{-\infty }^{x}f(t)dt =\int _{-\infty }^{x}{\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\exp \left(-{\frac {(t-\mu )^{2}}{2\sigma ^{2}}}\right)dt\quad $$

正規分布の累積分布関数

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
x = [-10+0.01*v for v in range(2100)]
y = [nd.cdf(v) for v in x]
plt.plot(x, y)
plt.show()

inv_cdf(p) 分位関数 (quantile function) 累積分布関数の逆関数

nd.inv_cdf(0.1) # => -1.5631031310892016
nd.inv_cdf(0.5) # => 1.0
nd.inv_cdf(0.99) # => 5.6526957480816815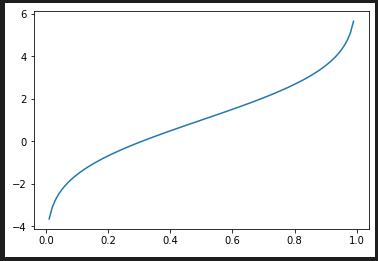

正規分布の累積分布関数の逆関数

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
x = [0.01*v for v in range(1,100)]
y = [nd.inv_cdf(v) for v in x]
plt.plot(x, y)
plt.show()

overlap(other) 2つの正規分布の確率密度関数の重なり

nd1 = statistics.NormalDist(0.0, 1.0)
nd2 = statistics.NormalDist(3.0, 1.5)

nd1.overlap(nd2) # => 0.22381671704369155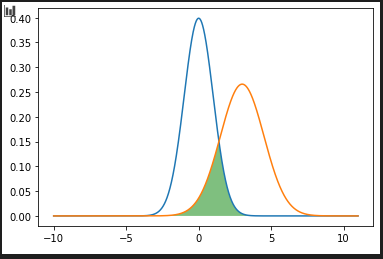

正規分布の重なり

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
x = [-10+0.01*v for v in range(2100)]
y1 = [nd1.pdf(v) for v in x]
y2 = [nd2.pdf(v) for v in x]
lap_y = [r if r <=s else s for r,s in zip(y1,y2)]
plt.plot(x, y1)
plt.plot(x, y2)
plt.fill_between(x,0,lap_y,facecolor='g',alpha=0.5)
plt.show()

sum([y*0.01 for y in lap_y]) # => 0.22381625164019625

quantiles(n=4) 確率密度関数を等確率になる位置で分割

nd.quantiles()
# => [-0.3489795003921634, 1.0, 2.348979500392163]
nd.quantiles(n=6)
# => [-0.9348431322034028, 0.1385454014090851, 1.0, 1.8614545985909148, 2.9348431322034028]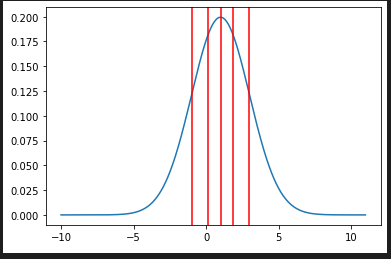

正規分布の確率密度関数の分割

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
x = [-10+0.01*v for v in range(2100)]
y = [nd.pdf(v) for v in x]
plt.plot(x, y)

quantiles = nd.quantiles(n=6)
ax.axvline(quantiles[0], color='r', linestyle='-')
ax.axvline(quantiles[1], color='r', linestyle='-')
ax.axvline(quantiles[2], color='r', linestyle='-')
ax.axvline(quantiles[3], color='r', linestyle='-')
ax.axvline(quantiles[4], color='r', linestyle='-')
plt.show()

zscore(x) 標準得点(z-score、standard score)　平均との差分を標準偏差を単位に見た大きさ

nd.zscore(0) # => -0.5
nd.zscore(1) # => 0.0
nd.zscore(2) # => 0.5
nd.zscore(3) # => 1.0

$$ z(x)={\frac {x-\mu }{\sigma }} $$

正規分布の変換

nd = statistics.NormalDist(1.0, 2.0)
nd # => NormalDist(mu=1.0, sigma=2.0)

nd*2 # => NormalDist(mu=2.0, sigma=4.0)
nd*3 # => NormalDist(mu=3.0, sigma=6.0)

nd+1 # => NormalDist(mu=2.0, sigma=2.0)
nd+2 # =>NormalDist(mu=3.0, sigma=2.0)

nd*2+1 # =>NormalDist(mu=3.0, sigma=4.0)