Python モンテカルロ法を使って円周率πを計算

2021-04-10

Pythonでモンテカルロ法(Monte Carlo method)を使った円周率πの計算を行う方法の解説です。

モンテカルロ法(Monte Carlo method)と面積

モンテカルロ法(Monte Carlo method)とは乱数を使ったアルゴリズムです。乱数を大量に生成しその結果を利用して確率や近似値を求めるのに使われます。

例えば、0以上1未満の乱数を2つ発生させそれを(x,y)座標とみなします。乱数が一様に発生していれば、点は1×1=1のサイズの正方形の中に均等に出現するはずです。ここで

$$ x^2 + y^2 < 1 \tag{1} $$

となる点を考えるとこれは半径1の円の右上1/4の点たちということになります。

点がある領域に出現する確率はその領域の面積の比率と同じはずなので、以下の式が成り立ちます。

$$ \frac{円右上の面積}{正方形の面積} = \frac{発生させた点のうち式(1)を満たしている点の数}{発生させた全ての点の数} \tag{2} $$

円右上の面積は$\frac{\pi}{4}$、正方形の面積は1なので、(2)の式から

$$ \pi = 4 * \frac{発生させた点のうち式(1)を満たしている点の数}{発生させた全ての点の数} \tag{3} $$

と計算できる事になります。

Pythonを使った計算例と図

モンテカルロ法円周率サンプル

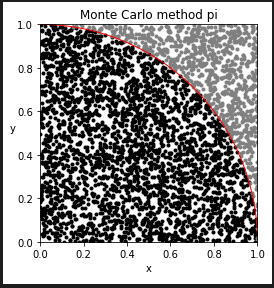
import random
import matplotlib.pyplot as plt

# 発生させる点の数
n = 4000

# 計算の再現性のため乱数のシードを設定
random.seed(0)

# [0,1)×[0,1)の点(x,y)をn個生成
point = [(random.random(),random.random()) for n in range(n)]

# 円の中に入る点を取り出す
point_in = [p for p in filter(lambda p: p[0]**2+p[1]**2 < 1, point)]
# 円の外に入る点を取り出す
point_out = [p for p in filter(lambda p: p[0]**2+p[1]**2 >= 1, point)]

# 式(3)から円周率を計算する
pi = 4*len(point_in)/n
print(pi) # => 3.137

# 以下図で表示を確認
fig = plt.figure()

ax = fig.add_subplot(1, 1, 1)

c = plt.Circle((0, 0), radius=1, fc="None", ec="r", linewidth=1)
ax.add_patch(c)

ax.set_title("Monte Carlo method pi")
ax.set_xlabel("x")
ax.set_ylabel("y", rotation=0)
ax.set_aspect("equal")
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)

ax.scatter([p[0] for p in point_in], [p[1] for p in point_in], marker=".", color = "black")
ax.scatter([p[0] for p in point_out], [p[1] for p in point_out], marker=".", color = "gray")